10+ 30 60 90 And 45 45 90 Triangle Rules
30 60 90 And 45 45 90 Triangle Rules. One angle must always be a right angle. If given the leg opposite the 30 degree angle, multiply by √3 to find the other leg, and multiply by.
 Conceptual Marketing Corporation From petrofilm.com
Conceptual Marketing Corporation From petrofilm.com
Consider the triangle of 30 60 90 in which the sides can be expressed as: Leave your answers as radicals in simplest form. Short side (opposite the 30 30 degree angle) = x x.
Conceptual Marketing Corporation
Construct a square four equal sides to the desired length of the triangle's legs; area = a² / 2. So the area of 45 45 90 triangles is: In a 45 ° − 45 ° − 90 ° triangle, the length of the hypotenuse is 2 times the length of a leg.
 Source: slideshare.net
Source: slideshare.net
- x 20 y 45° 2) a63 b 30° 3) x 72 y 45° 4) x y17 60° 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°). This type of triangle is also isosceles. Perpendicular (or height) = x. Perfect for a.
 Source: slideshare.net
Source: slideshare.net
Find the missing side of the given triangle. Perpendicular (or height) = x. A = \frac{1}{2}\cdot b\cdot h. The ratios come straight from the pythagorean theorem. Long side (opposite the 60 60 degree angle) = x√3 x 3.
 Source: mathmuir.weebly.com
Source: mathmuir.weebly.com
If the third value of the ratio n:n:n√2 is 4√2 then the lengths of the other two sides must 4. In our case, one leg is a base and the other is the height, as there is a right angle between them. 1) x 20 y 45° 2) a63 b 30° 3) x 72 y 45° 4) x y17 60°.
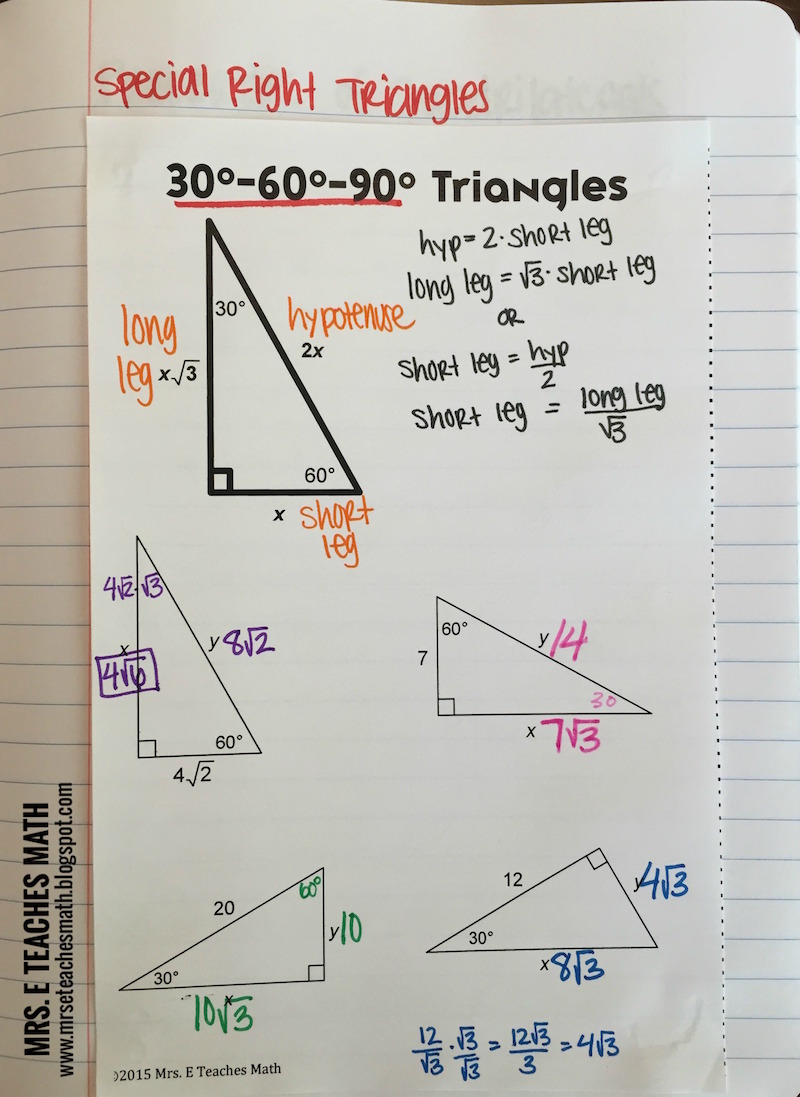
 Source: mrseteachesmath.blogspot.com
Source: mrseteachesmath.blogspot.com
There are two you'll need to be familiar with for the gre: Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x. Perfect for a high school geometry class! Long side (opposite the 60 60 degree angle) = x√3 x 3. You are given that the hypotenuse is 4√2.
 Source: petrofilm.com
Source: petrofilm.com
If given the length of the hypotenuse, divide by √2 to find the value the legs. A/c = √2/2 so c = a√2. Perpendicular (or height) = x. This type of triangle is also isosceles. 45 ° − 45 ° − 90 ° triangle is a commonly encountered right triangle whose sides are in the proportion 1:
 Source: petrofilm.com
Source: petrofilm.com
Perpendicular (or height) = x. If the third value of the ratio n:n:n√2 is 4√2 then the lengths of the other two sides must 4. If given the length of the hypotenuse, divide by √2 to find the value the legs. There are two you'll need to be familiar with for the gre: The measures of the sides are x.