35++ Area Of Triangle Formula Sin
Area Of Triangle Formula Sin. We identified it from obedient source. Area = ½ ab sin c.
 Downloads Crystal Clear Mathematics From crystalclearmaths.com
Downloads Crystal Clear Mathematics From crystalclearmaths.com
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. Area (∆abc) = ½ ab sin c. Area of a b m \triangle{a}{b}{m} a b m = 1 2 × a b × b m × sin ∠ a b m =\dfrac{{1}}{{2}}\times{a}{b}\times{b}{m}\times{\sin}\angle{a}{b}{m} = 2 1 × a b × b m × sin ∠.
Downloads Crystal Clear Mathematics
The formula used to calculate the area of the isosceles triangle by using the lengths of the equals sides and base are given as follows: Determine the area of a parallelogram in which two adjacent sides are 10 cm and 13 cm and the angle between them is 55 °. Area of triangle = a = ½ (b × h) square units. When one side is given.
 Source: crystalclearmaths.com
Source: crystalclearmaths.com
With this new formula, we no longer have to rely on finding the altitude (height) of a triangle in order to find its area. Find the area of triangle abc, given that the sides ab = 5 units, bc = 8 units and ∠abc = 60°. Formula of area of triangle. Determine the area of a parallelogram in which two.
 Source: youtube.com
Source: youtube.com
Area (∆abc) = ½ ab sin c. But since the given is an isosceles triangle (both sides are equal) then a = b =r hence, r^2. Area of triangle = (1/2) ⋅ (ac sin b) = (1/2) ⋅ (x) (14) sin 75. Area of triangle = a = ½ (b × h) square units. Only one triangle includes the.
 Source: youtube.com
Source: youtube.com
Sin ( a ) = opposite side hypotenuse = h c sin ( a ) = h c ⇒ h = c sin ( a ) substituting the value of h in the formula for the area of a triangle, you get r = 1 2 b ( c sin ( a ) ) = 1 2 b c sin.
 Source: mathswithgraham.org.uk
Source: mathswithgraham.org.uk
So we start solving it. List of formulas to find isosceles triangle area. Area = 2 ( 1 2 ( 13) ( 10) sin 55 °) = 106,5 square units. Now, if any two sides and the angle between them are given, then the formulas to calculate the area of a triangle is given by: It may be necessary.
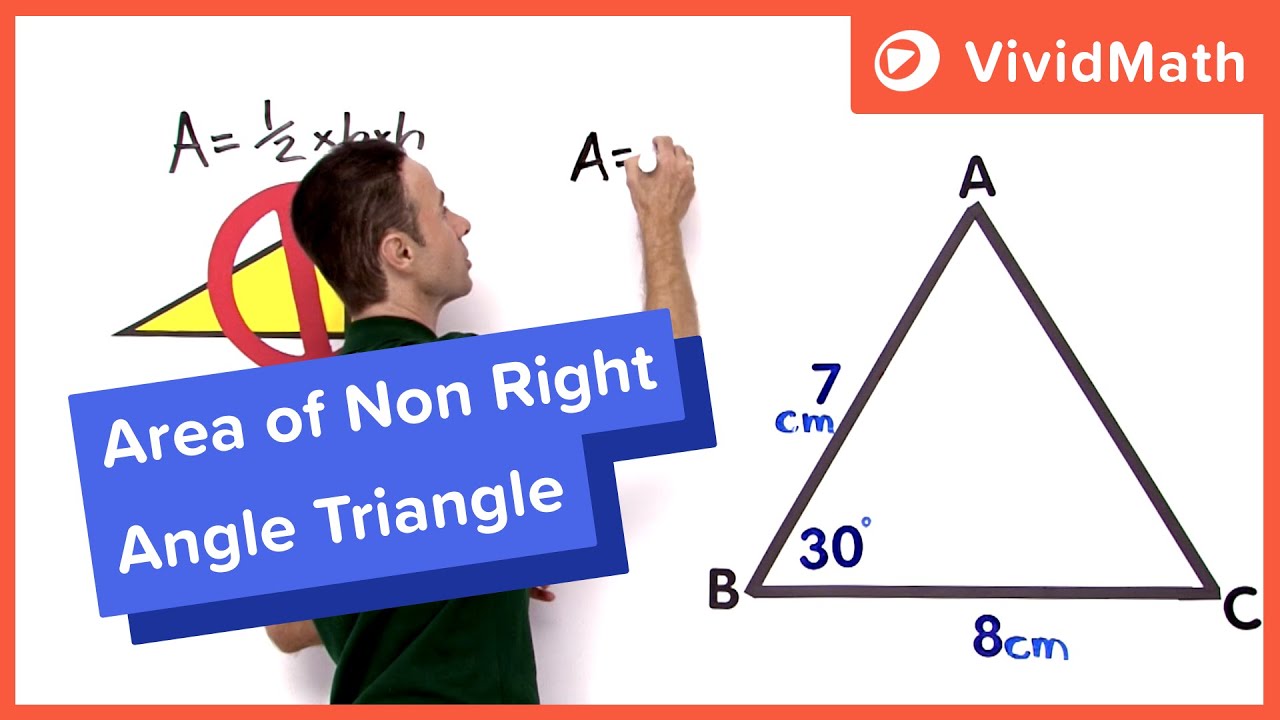 Source: youtube.com
Source: youtube.com
Area of triangle = (1/2) ⋅ (ac sin b) = (1/2) ⋅ (x) (14) sin 75. Area = 1 2 bc sin a. The formula used to calculate the area of the isosceles triangle by using the lengths of the equals sides and base are given as follows: Area δabc = 1/2 × a × c × sin (b) =.
 Source: andymath.com
Source: andymath.com
Area = ½ × (c) × (b × sin a) which can be simplified to: When base and height is given. Area = 1 2 bc sin a. The area area of a triangle given two of its sides and the angle they make is given by one of these 3 formulas: Sin ( a ) = opposite side hypotenuse.