20++ Area Of Triangle Formula Sine Rule
Area Of Triangle Formula Sine Rule. A = \frac{1}{2} a b sin(c). A s i n ( a) = b s i n ( b) = c s i n ( c) \frac {a} {sin (a)} = \frac {b} {sin (b)} = \frac {c} {sin (c)} sin(a)a.
 Integration Reverse of Differentiation Question 4 with From mathematics.laerd.com
Integration Reverse of Differentiation Question 4 with From mathematics.laerd.com
Sina a = sinb b = sinc c. Excelling learners will be able to solve unfamiliar problems using the formula for the area of a scalene triangle. The sine rule can also be used in deriving the following formula for the triangle's area:
Integration Reverse of Differentiation Question 4 with
Remember that the given angle must be between the two given sides. Cosine rule (the law of cosine): The area area of a triangle given two of its sides and the angle they make is given by one of these 3 formulas: A s i n ( a) = b s i n ( b) = c s i n ( c) \frac {a} {sin (a)} = \frac {b} {sin (b)} = \frac {c} {sin (c)} sin(a)a.
 Source: mathematics.laerd.com
Source: mathematics.laerd.com
Area of triangle = ½ ab sinc. Let us take a triangle abc, whose vertex angles are ∠a, ∠b, and ∠c, and sides are a,b and c, as shown in the figure below. It allows us to find the area of a triangle when we know the lengths of two sides and the size of angle between them. The area.
 Source: slideserve.com
Source: slideserve.com
The second equality above readily simplifies to heron's formula for the area. Cos 90° = 0 so if a = 90°, this becomes pythagoras’ theorem. Let us take a triangle abc, whose vertex angles are ∠a, ∠b, and ∠c, and sides are a,b and c, as shown in the figure below. Find the area of triangle pqr if p =.
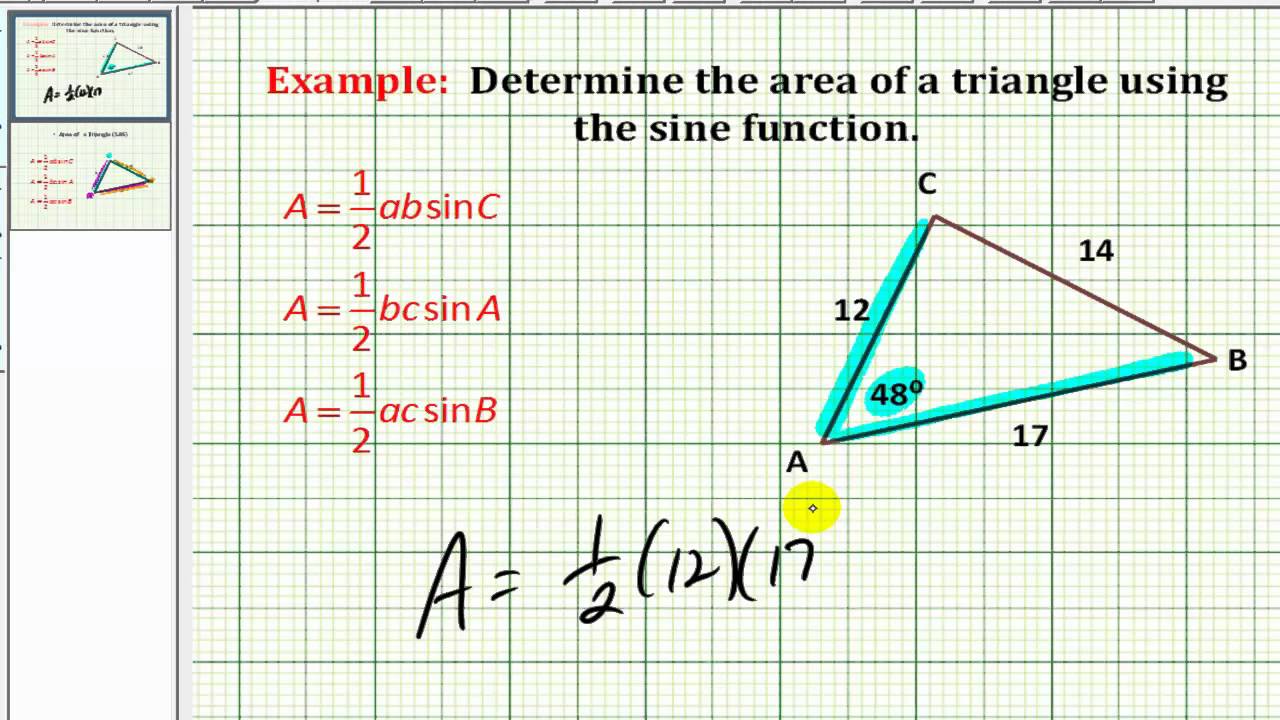 Source: youtube.com
Source: youtube.com
Remember that the given angle must be between the two given sides. Area rule sin rule formula: Sin sin 6.89 da a sin100 13 rearranging gives: The area rule states that the area of any triangle is equal to half the product of the lengths of the two sides of the triangle multiplied by the sine of the angle included.
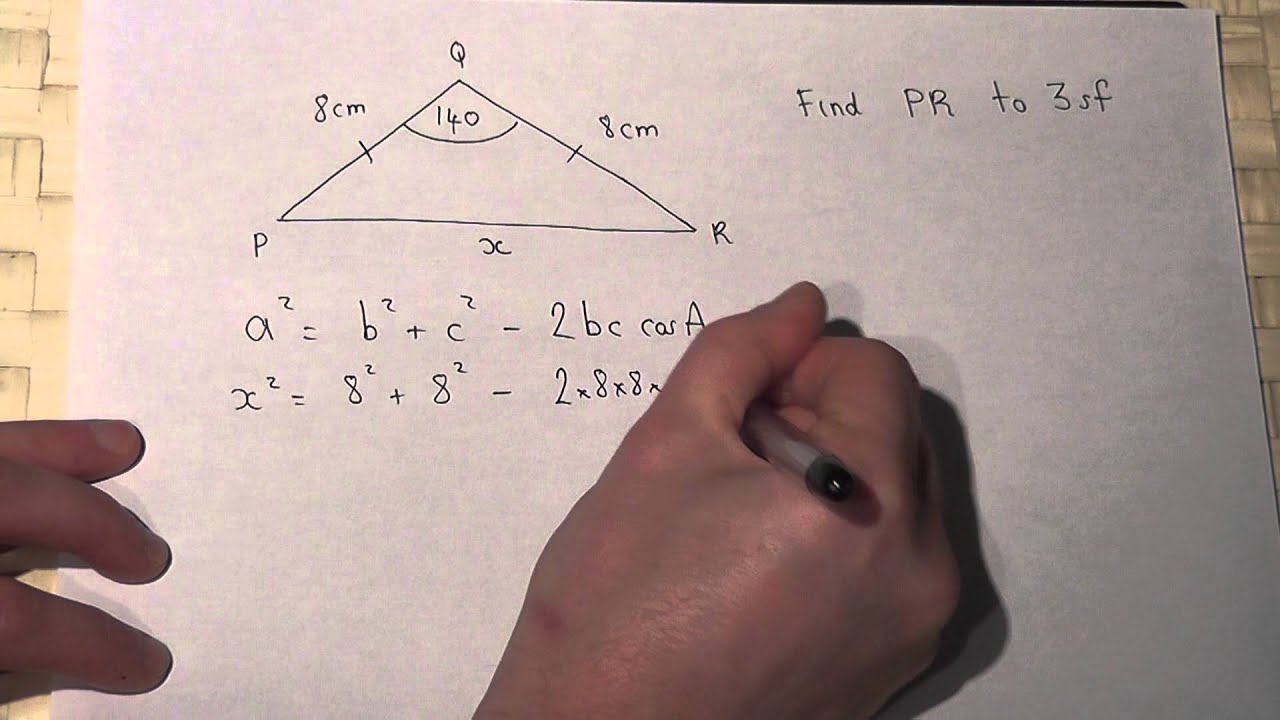 Source: youtube.com
Source: youtube.com
Developing learners will be able to calculate the area of a scalene triangle. The area of a triangle using sine. Sin sin 6.89 da a sin100 13 rearranging gives: \ [area = \frac {1} {2} \times bc \times \sin a] \ [area = 0.5 \times 3 \times 7 \times \sin (35^\circ )] \ [area = 6.02255.] \ [area = 6.02c.